A Deep Dive into Linear Regression

Hello curious minds! If you're venturing into the vast world of machine learning, understanding linear regression is a crucial first step. In this post, we'll go beyond the basics and delve deeper into the intricacies of this foundational algorithm.

Introduction: What is Linear Regression?

Linear regression is a supervised learning algorithm that models and analyzes the relationships between a dependent variable and one or more independent variables. The main goal is to find the linear relationship between the input (independent variables) and the output (dependent variable).

Visualizing Linear Regression

Imagine you scatter plot data points on a graph. Linear regression, in essence, draws a straight line that best captures the underlying trend of those points.

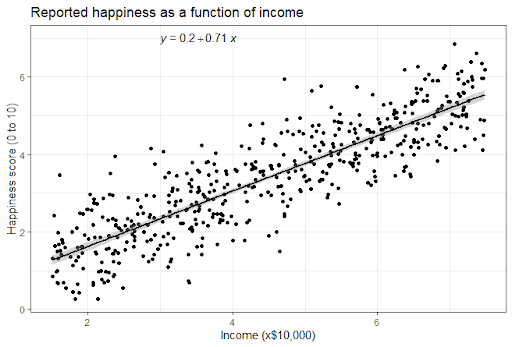
The Mathematics of Linear Regression

The equation for simple linear regression is:

Where:

• $y$ is the dependent variable (what we're trying to predict),
• $x$ is the independent variable (input),
• $\beta_0$ is the y-intercept of the line,
• $\beta_1$ represents the slope of the line, and
• $\epsilon$ represents the error in prediction.

The objective is to find values for $\beta_0$ and $\beta_1$ that minimize the error $\epsilon$.

Cost Function and Gradient Descent

The 'best fit' line is found by minimizing the sum of the squared differences (errors) between the predicted outputs and actual outputs. This method is termed the "least squares method."

The function used to compute this error for all observations is called the "Cost Function" or "Loss Function". Once we have our cost function, we can use a method like "Gradient Descent" to find the minimum of the function, which would give us the best possible line.

Assumptions in Linear Regression

For linear regression to work optimally, certain assumptions are made:

1. Linearity: The relationship between independent and dependent variables is linear.
2. Independence: Observations are independent of each other.
3. Homoscedasticity: The variance of errors is consistent across all levels of the independent variables.
4. No multicollinearity: Independent variables are not too highly correlated.

Applications of Linear Regression

Linear regression finds applications in diverse fields, from predicting sales, assessing medical risk factors, to financial forecasting, and more.

Limitations

While powerful, linear regression does have limitations. It assumes a linear relationship between variables, and outliers can have a disproportionate effect on results.

Conclusion

Linear regression is a foundational stone in machine learning, offering both simplicity and utility. While it might seem basic, it lays the groundwork for understanding more complex algorithms and techniques in the future.

Stay curious and keep exploring!